This landscape was generated entirely through VEX, no off-the-shelf tools used at all. This was the final project in the CGMA, “VEX in Houdini” course.

Systems implemented:

Height Field Generation (with Domain Warping)
Thermal Erosion (aka Thermal Weathering)
Hydraulic Erosion
Volume Advection
Volume Displacement

The coloring is also all done via VEX code, including the sides of the landscape block as well as the water surface.

Landscape Height Field Generation

The first step I had to go through was generating the base landscape. To do this, we used an FBM (Fractal Brownian motion). FBM’s are described in a lot more detail here and even better here (visual examples!), but to put it simply it is a noise function being run through a loop, with each loop introducing additional detail.

We call the stages of this loop ‘octaves’ and typically increase or decrease, and shift or otherwise manipulate the noise pattern every octave.

We control how each octave changes with a series of parameters we expose, allowing us to directly edit different parts of the equation. The common attributes to control are:

Amplitude, Frequency, Lacunarity, Persistance, and number of Octaves.

In addition to those however, we also went further and added Domain Warping (mentioned near the bottom of the second link about FBMs above). Domain Warping allows us to modulate the generated terrain to create even more organic and unique formations. This is done by using ANOTHER FBM to warp the previous one, this leads to some pretty compelling effects.

Each of these attributes gets demonstrated briefly in the following video:

So there you have it, that single FBM wrangle is responsible for the entire base landscape. The color is coming from the ‘terrain_vis’ subnet, which only contains the following:

In order, these nodes are pulling in the ‘height’ attribute from the FBM node above, using that to do the actual vertical displacement of the grid, and then applying a color gradient from the lowest point to the maximum height, all before making sure the normals are set for the vertices and passing everything down to an output node so I can grab it later if needed.

Erosion

As a quick overview, what we’re doing with Erosion is calculating how the height of each point on the grid will change over time. We’re doing this with 2 separate equations, one that mimics the effects of Thermal Weathering (sediment sliding down mostly by gravity/friction), and another that mimics the effects of Hydraulic Erosion (sediment being carried down a slope by a constant rain / evaporation cycle). When utilized together and balanced properly, these can create a very natural looking landscape.

If you’re interested in a deep dive into these equations and their origins / development, check out the following technical papers:

• Realtime Procedural Terrain Generation: Realtime Synthesis of Eroded Fractal Terrain for Use in Computer Games
by Jacob Olsen, Department of Mathematics And Computer Science (IMADA), University of Southern Denmark

• Fast Hydraulic Erosion Simulation and Visualization on GPU
by Xing Mei, Philippe Decaudin, and Bao-Gang Hu

• Fast Hydraulic and Thermal Erosion on the GPU
by Balázs Jákó, Department of Control Engineering and Information Technology Budapest University of Technology and Economics Budapest/Hungary

Much of the implementation we designed is based on the successful implementations of these technical artists. The papers also go into some additional details such as enhancing sea-floor generation through additional equations that were not implemented here. Definitely check them out!

That intro out of the way, let’s look at the first part of the graph, the Geo level:

As the box label explains, what is happening in the top portion of this graph is being saved to the disk, and then re-imported as a static file before getting passed on for further processing. This is set up this way because the Erosion equations function over time, and therefore need to be compartmentalized as a Solver. This allows us to run the equation over the frames of our animation timeline, the ‘Timeshift’ node then lets us freeze the result at the frame we like, and the ‘Rop Geometry’ node saves this to disk. Breaking up the process like this means we won’t need to sit and wait for the whole terrain to re-bake everytime we close and re-open the file, or make changes further down the pipe. It also means we can go back, make changes, and save a new version out to the disk and have the information further down the pipeline be maintained.

Now let’s look at the real heart and soul of this exercise, the Solver:

There’s a lot going on in this solver, and I’m not going to get too boring and post a wall of code for each node, but I do want to visually show a little bit of what each section is doing on its own and explain through how each part in turn works together. Before that, a few basics:

Erosion 101

Again, for the really technical explanation, check out the papers I mentioned above, but the summary: What we’re going to do here is create a series of ‘virtual tubes’ between each point in our grid, and then make it so ‘sediment’ can ‘flow’ between them. I use quotes because the concepts are little more abstract than that when working with the code, however that’s effectively what the system is doing. Each step through the solver, each point looks at all its neighbors, figures out what’s up and what’s down, what the slope of the hill is where it exists, and how much water is flowing over it.

Solvers 101

Just to make sure I’ve covered all the bases we’ll start at the very top. The switch node is just handling the very first beat of the solver, where it switches from the start frame to taking in the subsequent frames. This ensures that the equations are calculated on the data output from each previous frame, and not just calculated on the data from the first frame every time.

Slope Calculation

We’ll start with the details here. The Slope Calculation node is calculating a cross product (perpendicular vector) between 2 vectors that are defined by neighboring points. After calculating this vector, we can subtract it from 1 to get the slope we need. If mapped to a color output, the resulting values will resemble a Curvature map.

Sketch of what is calculated in this first wrangle. The green arrow is the cross product of the red and the blue arrows. We calculate the green arrow and subtract it from 1, for every point in the grid.

Slope values mapped to Cd (basic surface color). Debug view of slope values over landscape. We can use this later on to enhance the final colors as well.

Make it Rain

Now that we have the slope information stored, we need to introduce water. Lots and lots of water. These next 3 nodes I’ve colored blue are going to handle basically all the water calculations in our solver. The first node literally just makes a float variable called ‘rain’ and sets it to 1.0.

Next, the flux calculations. This is going to determine how much water should flow in what direction. This is calculated by comparing each point to each of its neighbors again, in a similar fashion to how we checked the slope earlier. Instead of determining simply ‘how much am I sloped?’ however, this is more of a ‘how much higher / lower am I than each of my neighbors?’. This is what really makes the water flow in the right directions at all times and prevents it from flowing uphill. With the flux calculated, determining the velocity of the water flowing through the point becomes possible. Visualizing this is over time magical:

Visualization of the Flux Velocity vectors animating over time.

Of course, like all good debug views, this is much better when mapped to our texture with some color in it:

Well that’s pretty awesome, but here’s one more just so you can see what’s happening by itself:

You can actually see the flow! Absolutely blew my mind when I hit play and saw this happening. I never expected the math to produce such an effective result, but there it was. And this is still such a simple version compared to some of the tools made by teams at SideFX or Quadspinner, it really is astonishing to see what a little math can do when its set on the right path.

Erosion and Deposition / Sediment Transport

The next 2 nodes are dictating how much the height is allowed to change for each point. We accomplish this by setting up a ‘transport capacity’ that is determined by a user defined capacity, multiplied against the flux speed, amount of water, and slope at any given point, at any given time. We also define how much of the height can be ‘dissolved’ and how much can be ‘deposited’ into and out of this transport capacity when it is moved to the next point (via our ‘virtual tubes’ in the direction of the flux flow). In action this looks pretty cool, but we can also see how fragile the equations become, and how critical it is to balance the system:

You can see the brightest areas above as indicators of trouble brewing. Not long after it reaches that “ultra-saturation” point does the system start to fail. To fix this, we add the next little piece of the puzzle:

Evaporation

This wrangle has one single line of code, where we update the total amount of water in the system by multiplying it against a global evaporation rate, determined by the user. In my case I settled with a rate around 7% evaporation (.07) to get a comfortable result, which meant each frame the total amount of water at every point was multiplied by 0.93, steadily reducing it from what would otherwise be a constant flow, resulting in the issues we saw before.

With the rate set and properly balanced through trial and error, we end up with something like this:

Water Flow Debug view, now with less flooding!

Looking good! That covers the breakdown of the hydraulic erosion, next up:

Thermal Erosion

Thermal erosion is a much simpler system, though there are still some equations behind it all. Again, for the most detailed look at the math, check out the papers mentioned at the top of the section. I’ll just be giving the briefest of high level explanations of what’s happening in these nodes.

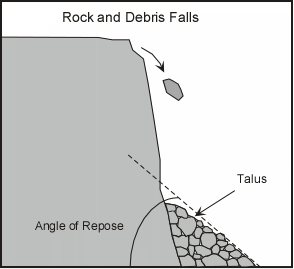
The real-world phenomena we are trying to replicate is the breakdown of material and collection of piles of Talus, or Scree (to those hikers of you reading this), at the base of the hills. If you’ve ever seen a mountain, or even a sorta big hill, you’ve probably witnessed this.

The Angle of Repose (also referred to as the Talus Angle in the papers above) is ultimately the data we want the user to be able to define. Note: To protect the more vertical elements often found in nature would require additional equations for Mesa formation that our system does not get into, so our thermal erosion will act instead as a universal erosion, rather than just on ‘weakened’ surfaces as it might in the real world, depending on the softness of the underlying rock/earth. This means that instead of seeing this:

We get something more like this:

Which still isn’t bad, the effect is nice and there are areas in the world where the earth might be softer and formations like this occur. Note how in this example, we can really see how the height is maintained, but the slopes of the forms are all ‘spread out’ until they all have reached that Talus Angle we defined, in a uniform manner across the entire surface.

With the two systems working in tandem we can achieve the resulting terrain in the final image at the top of this post. The only other step was to increase the resolution of the grid, generate an interesting base landscape, and let the system do its thing! Of course while tweaking values and seeing what looks good as you go.

This post ended up way longer than I had anticipated so I’ll be saving the breakdown of the Clouds and the Water shader for another time, so until then, thanks for reading!

Houdini Vex Exercise - Erosion